Intro
As part of the courses I am taking, I learned about something I guess I, as a “computer engineer”, should have come across earlier; but well, it would seem I didn’t.
I’ll just show 3 examples anyone can easily find out there on the Internet, of things that happen with floating point operations. Obviously for the purpose of this blog, I’ll be using R.
(The rest of my weekend I’ll be trying to personally understand precisely how this all works (but not for the Blog, as the explanations I am studying with the University).)
So this entry is just about being aware of it, not about explaining the why’s and how’s, as that’s a rather long topic. Also, it’s easy to program the examples, not as easy to explain exactly the workings of the computer behind the scenes 🙂
All in all, if this Blog entry serves only to pique someone’s interest so that they can look into the MSc degree I have just started to attend sometimes in the future, it’ll be a job well done.
Imprecisions
In summary, computers sometimes round numeric values, one way or another, because of how they store numbers (particularly, floating point numbers). And for things that have very similar amounts of significant digits, operating with two numbers that are very similar (or very dissimilar) can sometimes have quite an impact.
Examples
The easiest one, and my first surprise when discovering the topic:
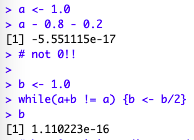
So well, two things apparently equal (to us), like 1 and (0.8+0.2), can be “very similar” for the computer. And when two things are “almost equal”, well, things get weird.
Also, it would seem you can reproduce those in Python on similar computer architectures… And that’s due to the IEEE 754 standard for 64bits double precision floating point representation.
The value of b in the calculations above is the threshold at which apparently our computer understands it is so small, it considers it negligible, so that a+b = a becomes true. So it can be seen as the minimum distance between two floating point numbers our computer will take into account.
Not only for very small values
Operating with big values that are very similar, things happen too. Here is an example that I am now translating into R code and demo-ing in R.
So moving from one version of the formula (left side) to the next (right side of the equation), step by step (you’re welcome), would look like so (thanks LaTeX):
![]()
Two mathematically equivalent functions will have different errors once run in R, in this case for bigger values of x. And that is because things will get very similar with limited precision. In such cases, maybe avoiding substractions can help…
Using the mosaicCore package discovered last week, we can now express these like so:
library(mosaicCore)
library(plyr)
f1 <- makeFun(sqrt(x) * (sqrt(x + 1) - sqrt(x)) ~ x)
f2 <- makeFun(sqrt(x) / (sqrt(x + 1) + sqrt(x)) ~ x) # equivalent to f1
my_function_compare <- function(in_func1, in_func2, e_range, s_step) {
rbind.fill(lapply(10^seq(e_range[1],e_range[2],s_step), function(i) {
data.frame(x = i, f1_x = sprintf("%.18f", in_func1(i)), f2_x = sprintf("%.18f", in_func2(i)))
} ))
}
my_function_compare(f1, f2, e_range = c(0, 15), s_step = 1)
Which gives the following results:
> my_function_compare(f1, f2, e_range = c(0, 15), s_step = 1)
x f1_x f2_x
1 1e+00 0.414213562373095145 0.414213562373095090
2 1e+01 0.488088481701514754 0.488088481701515475
3 1e+02 0.498756211208899458 0.498756211208902733
4 1e+03 0.499875062461021868 0.499875062460964859
5 1e+04 0.499987500624854420 0.499987500624960890
6 1e+05 0.499998750005928860 0.499998750006249937
7 1e+06 0.499999875046341913 0.499999875000062488
8 1e+07 0.499999987401150925 0.499999987500000576
9 1e+08 0.500000005558831617 0.499999998749999952
10 1e+09 0.500000077997506343 0.499999999874999990
11 1e+10 0.499999441672116518 0.499999999987500054
12 1e+11 0.500004449631168080 0.499999999998750000
13 1e+12 0.500003807246685028 0.499999999999874989
14 1e+13 0.499194546973835973 0.499999999999987510
15 1e+14 0.502914190292358398 0.499999999999998723
16 1e+15 0.589020114423405183 0.499999999999999833
And I just think this is beautiful. The math is sound, but knowing how to choose one way or another to express the equation into code will make a whole lot of a difference!
Conclusions
There are things to be done to reduce the compounding of errors due to computers limitations in certain circumstances, by better understanding of how those errors appear and how they interact.
This is not too straightforward, but I’m excited to dive deeper into these things and really get to understand it all. (That I actually get there, is another question :))