Intro
A real quick post about a couple of math (matrix) details, and a trick with rational numbers with R.
Inverse of a Matrix
Mathematically, getting to the inverse of an “nxn” matrix A means finding an nxn matrix B such that A • B = I, where I is the nxn Identity matrix.
Easier said than done, when doing that by hand (look around for example for the Gauss-Jordan method for a 3×3 matrix, and you’ll see what I mean), but maybe we don’t need to make it that complex, right? In R, getting to the inverse of a matrix is not complicated, you just need to use the solve() function.
Of course, you need a square matrix (otherwise multiplying it by a matrix with the same dimensions will not work).

Then the matrix must be non-singular. If a matrix is singular, it has a determinant 0, but it also means that some combinations of its rows or columns can be used to get a 0 vector, and that means that such rows or columns do not each bring new information to the system.
In the next example, the columns are rather clearly linearly dependent vectors (column 1 + column 3 – 2*column 2 = 0), and so the determinant will be zero. Which is equivalent to say that there is no inverse matrix for that case.

The trick: Human-readable fractional values
Now if the matrix is non-singular and square, one can use the “solve()” function in R:
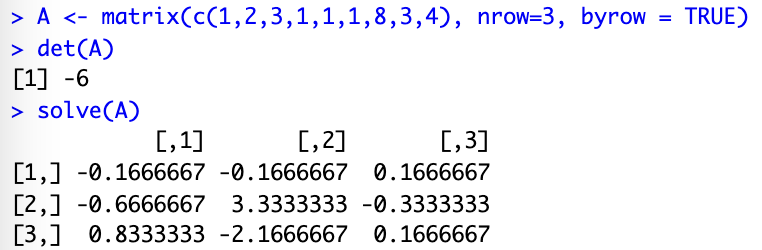
The only issue with it is, it shows it’s done by a computer. And for a human, well, it isn’t all as practical/readable as one might wish. Sure, you probably can recognise those 0.66666667 as 2/3, or 0.333333 as 1/3, but it gets trickier for 0.8333 or -2.16667, doesn’t it?
As my needs about what I ask from R are evolving because of one of the University courses I’m taking, I found the “fractions()” function that came in very handy:

And that’s it!
Note: You might recognise that the determinant (in the case above it was -6) might play a role in the denominator of these fractions there, and then maybe you will grasp a hint about why it’s sooo important that the determinant of the matrix is non-zero to be able to calculate the inverse of a matrix in the first place 🙂 If you don’t see it clearly in the above, maybe this next example will make it more visual:

The easier case
For a diagonal matrix, we know it’s going to be non-singular upfront (you can’t obtain one row from combinations of the others, and the same goes with the columns). But what’s more interesting regarding the inverse is that’s it’s rather easy to find:
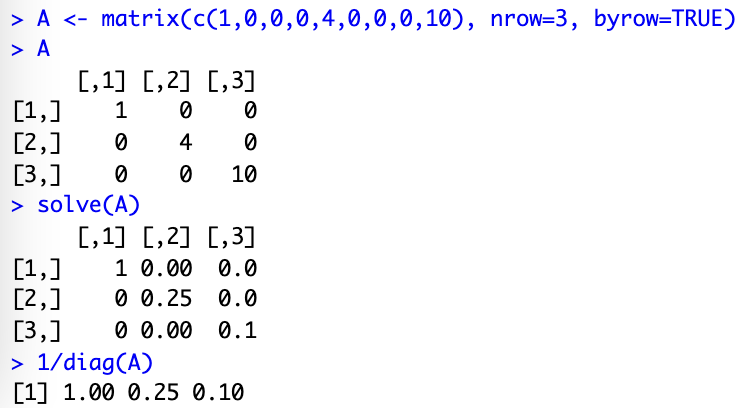
That particular case was important because initially, a few weeks back, I’m ashamed to admit (and I probably shouldn’t!) that I didn’t remember how to calculate the inverse of a Matrix, and I almost made the mistake to extrapolate the rule of “1/(matrix element)”, because the first exercise I was faced with had a diagonal matrix… Thank goodness I questioned myself there (something was too easy), I ran more checks and studied some more, which saved me moving forward…
And that’s why to me it’s important to understand why we do the things we do in math, instead of knowing only the “how”.
What about irrational numbers?
Glad you asked. By definition, irrational numbers cannot be expressed with a division of two integers. So what would the fractions() function from the MASS package do with, say, Pi or Euler’s number?
Well, it will get you to an approximation, with potentially more precision if you ask for it (but then again, there is no real point to it, I’d say… It’s just fun to see it 🙂 )

Conclusions
Well, I made a long post out of a very simple thing: There is an R package, MASS, with a function called fractions() that will find a nice fraction for rational values for us.
References
MASS::fractions() documentation
Explanations of why one could want to use the calculation of an Inverse