Intro

This time around, I keep going studying and implementing optimization algorithms, based on the already mentioned reference book, and I want to work on a slightly different family of these, now a full blown “metaheuristic” in fact, called “Genetic Algorithms”.

As this one is a bit different, I will take my time, and go bit by bit. So today is about “setting things up” (mostly).

Harder minimization

This time, we will try to minimize this function (see visualization), which would be quite hard for (say) Gradient Descent (it most probably wouldn’t find the global minimum at all).

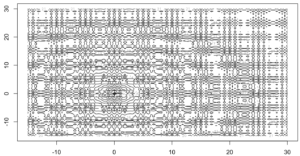
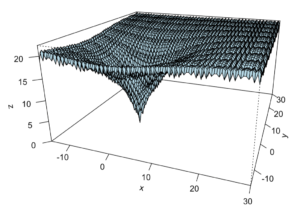
Algorithm Overview

As usual, I am not inventing anything. Not only am I using a book for reference pseudo-code, but of course these algorithms are documented all over, say for instance in Wikipedia.

Overall, the idea is to start with a “population of individuals” (each representing a possible solution in the search space). Then individuals are selected as parents, have one or more children, which can also suffer (in theory, rarely) mutations (which allows to explore more of the search space).

This leaves us with a bigger population of individuals. At this point, we stop concerning ourselves with parents or childrens and consider them all as individuals.

A new “generation” is then “selected” (in reference to “natural selection”) using (normally) the fittest individuals (e.g. minimum values) from that bigger pool of individuals, and then the process can start anew.

The selection of parents can be done in several ways, the mix of parents “genes” into each child can follow some process (usually varying say the proportion & redistribution of each progenitor’s genes), and mutations can happen more or less often (through a parameter, typically).

The algorithm stops when it “converges” (or after a set number of generations), whereby the best individual in the final generation is representing the best found solution (hopefully, a global minimum, in our scenario).

Binary encoding of individuals

Although there are alternatives, the simplest approach is to use “binary genes”. As numbers can – obviously – be binary encoded, all we have to do is encode the search space (min/max ranges for say x, y coordinates) so that given a number of bits per coordinate, any value stays in range, and any individual will be a binary representation of two (in our example) such coordinates.

As the fitness corresponds to a real value, we then just need to have a “decoder” of the binary values to evaluate the objective function to minimize using real numbers.

At this stage of the development, I have ensured I can generate the “search space” visually (similar to recent blog entries), but also that I can generate such individuals, and maybe even a “generation”.

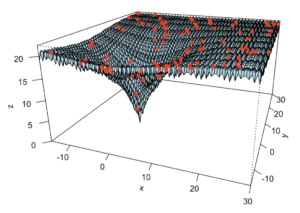
Code for today

This is all provided in my GitHub.

As this is a bit “messier” with more concepts than most recent entries, I chose to create for myself an RStudio Project, whereby I can then source files with relative paths… And so the code for today requires two files (*_v001.R).

Next time

Well, in upcoming entry/ies, I shall code for selecting parents, generating children, mutation, and iteration across a number of generations, thereby in principle closing the loop on this particular topic of Genetic Algorithms applied to optimization.