Intro
I’ve mentioned I’m looking for a subject for my project, and that one of the concepts I’d like to leverage is what’s commonly called “Operations Research”, also known more generally as “Optimization”.
Of course, I want to use R for it 🙂
And so I chose a course about that. The course has started, and there are some initial exercises to be delivered (for now, rather introductory, it will get harder…). Now “R” is not a chosen alternative officially for the course, but I am authorized to use it. And so I shall.
This here is a sample of one of the initial exercises. As the exercise is mostly about reproducing something that already is detailed, I feel I am breaking no rule by creating an alternative solution (it’s really a very mainstream example), plus I’m doing it here in another programming language.
So here goes.
The exercise
“A manager has to decide how much time to allocate between radio and TV advertising.
- At least 70% of the time should be allocated to TV.
- The audience exposure per minute is 150 users for radio and 800 users for TV.
- The cost per minute is 400 € for radio and 2,000€ for TV.
- There is an available budget of 25,000€.
- How many minutes should the manager allocate to each medium if she wants to maximize audience exposure?”
The math
The only difficulty of the above exercise is how to express that “70% of the time” should be allocated to TV.
If “x1” is Radio time, and x2 is TV time, we want to make sure that x2 >= 0.7 (x1+x2)
One trick we will use is to change a “greater than” constraint into its negated version, thereby getting to a “lower than” constraint. With some re-work, we can get to the second of the inequalities shown below:

The code
So now we’re about ready to implement this in R. This time around, we will test the boot package, and its implementation of the simplex() function.
a<-c(150,800) # Objective function's Coefs. # m1*n coefs (lhs) <= constraints #A1<-rbind(c(400, 2000),c(0.7, -0.3)) # Alternative A1<-matrix(c(400, 2000, 0.7, -0.3),nrow = 2, ncol=2, byrow=TRUE) b1 <- c(25000,0) # Vector m1 (rhs) <= constraints. A2 <- NULL # m2*n coefs (lhs) >= constraints b2 <- NULL # Vector m2 (rhs) >= constraints. adv_alloc_simplex_res <- simplex(a=a, A1=A1, b1=b1, A2=A2, b2=b2, maxi="TRUE") # Maximize Objective. adv_alloc_simplex_res
One of the reasons to set all the inequalities with “lower than” configurations was because certain R packages do not accept “greater than” comparisons. As they are in fact equivalent with a simple multiplication by “-1”, all is good for us here. Here the corresponding output (it is the right answer with the selected conditions):

So you should really choose to go all in with the TV budget, with 12.5 minutes in total, for a maximized audience of 10K viewers.
Visually, the matlib package includes some alternative for simple scenarios like this one to visualize the result:
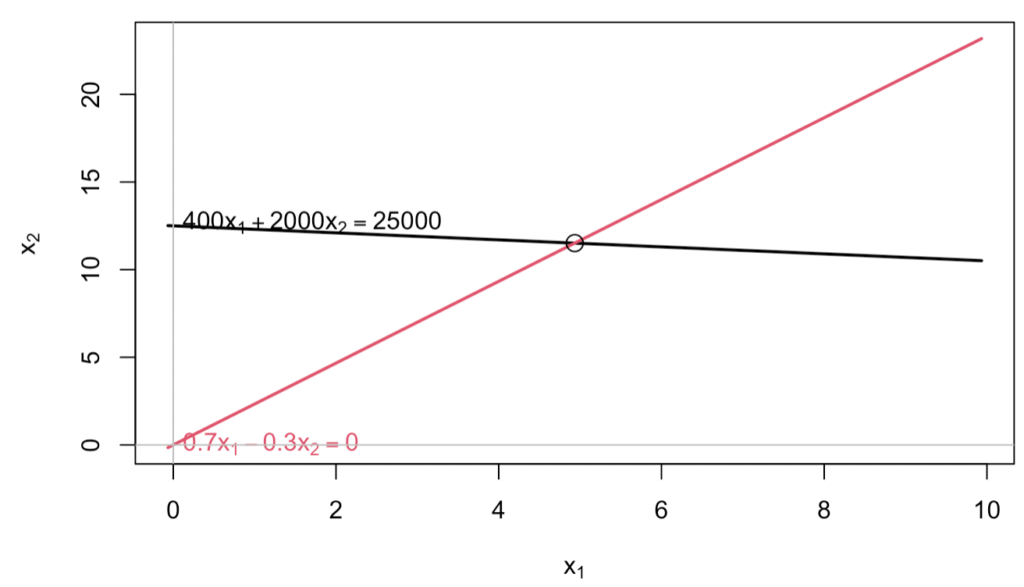
Conclusions
This concludes our first tentative at doing Operations Research in R 🙂
It’s not too difficult. Really as it often happens in these cases, making sure you get the equations and inequalities right will be key, as the code itself is not too complex.