Intro

So I keep going with the reference book for a while. BTW, the book can be found here (NOT a referral or anything, I don’t make money out of this, it’s just a pointer to one place you can find it). And yes, the book is in Spanish…

So one of the first algorithms (beyond “random search”, I guess) is the well known Gradient Descent. Let’s implement that in R.

R-based Gradient Descent for bi-variate function

The code for today can be found here.

The Gradient Descent method (to look for a minimum value, say) is fine for mono-modal (convex) functions that are twice differentiable (in theory at least), in spite of being reasonably slow in converging.

A numerical method is easy to implement in this case. Let’s have a look at what it looks like:

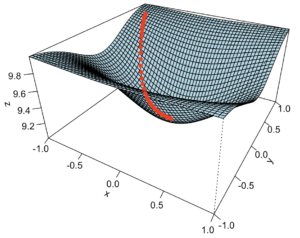
Why is Gradient Method important, you ask? Well, at least for what I learnt some time ago, let’s just say it’s used in ML for instance to tune neural network through back-propagation. And of course that’s just one example (but a very common application these days). One could also use it to minimize (or well, maximize) any compatible functions, of course, and so this has application in Operations Research at large, obviously.

One draw-back

One of the limitations of the Gradient Descent method is that it works fine for mono-modal functions (in the search space at least, that is), but it can’t avoid falling into local minima if the starting point goes in that direction…

Next time

I’ll try and implement the next proposed algorithm, “Simulated Annealing”, that helps with looking for global minima.